AfD — Vergleich von Berichterstattung und Umfrageerfolg
Analyse der Umfragewerte der AfD im Vergleich mit der Berichterstattung
Eine Untersuchung von Umfragewerten der AfD und der Berichterstattung über die Partei. Die Analyse wurde in Python mit der Pandas-Library in einem Jupyter-Notebook erstellt. Im Folgenden ist schlicht das Notebook wiedergegeben.
Achtung: Das Projekt wurde an zwei Tagen ausgearbeitet und ist hauptsächlich als Lernmaterial für Datenanalyse mit Python gedacht.
Prämisse
Ich vermute, dass die Umfragewerte der AfD durch (überproportionale) Berichterstattung präzediert werden.
Daten
Die Umfragewerte sind der Sonntagsfrage von Infratest Dimap entnommen. Als Maß für die Berichterstattung wurde der Google-News-Trend „Alternative für Deutschland (Politische Partei)“ gewählt.
Hier ist zu beachten, dass Google die Berechnung des Trends innerhalb des gewählten Zeitraums geändert hat.
Vorgehen
Die wöchentlich (Google) bzw. zweiwöchentlich (Infratest) erhobenen Daten werden in monatliche Mittelwerte umgewandelt und im Zeitverlauf dargestellt. Zur Untersuchung der Korrelation werden die Daten zunächst auf das Intervall [0,1] normiert. Anschließend wird der Google-Trend schrittweise um einen Tag relativ zur Sonntagsfrage verschoben und die Verschiebung gewählt, die die höchste Korrelation herstellt.
Eine leichte Säuberung der Daten ist nötig, da die Berichterstattung über die AfD Ende 2013 stark ausreißt.
|
1 2 3 4 5 |
import pandas as pd import matplotlib.pyplot as plt import numpy as np %matplotlib inline |
|
1 2 3 4 |
#reading the two csv files google = pd.read_csv('GoogleNews-DateTrend.csv', delimiter=";") infra = pd.read_csv('Infratest-DateValue.csv', delimiter=";") |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
#Converting the date formats in the files to a standard one infra['Date'] = pd.to_datetime(infra['Date'], format="%d.%m.%y") google['Date'] = pd.to_datetime(google['Date']) #Setting the date column as index infra.set_index(['Date'], inplace=True) google.set_index(['Date'], inplace=True) #Combining the two datasets with the 'outer' method since the dates of the two datasets do not align. full = infra.join(google, how='outer') #Taking 4-weekly buckets and average over them instead of the daily results given from Google and Infratest full_resampled = full.resample('4W').mean() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
#Plotting the full dataset, setting as a function first def plotData(dataset, secondaryData, leftLabel, rightLabel): plt.figure(figsize=(20,20), dpi=300) ax = dataset.plot(secondary_y=[secondaryData]) ax.set_ylabel(leftLabel, color='g') ax.right_ax.set_ylabel(rightLabel, color='b') ax.grid(color='k', axis='x', which='both') ax.grid(color='g', axis='y') ax.right_ax.grid(color='b', axis='y') ax.legend_.remove() plotData(full_resampled, secondaryData='Infra', leftLabel='Google News Trend', rightLabel='Infratest Sonntagsfrage') |
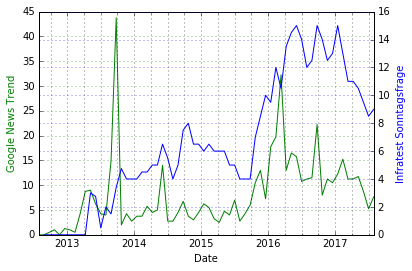
Diskussion des bisherigen Ergebnisses
Wir beobachten einen starken Peak der Berichterstattung über die AfD im September 2013. Wir betrachten daher nur Daten ab 2014, ein punktweises Entfernen des Peaks erscheint unnötig, da er nah am Beginn des Datensatzes liegt.
Offenbar korrelieren die Verläufe aber relativ stark.
|
1 2 3 |
#Removing the outlier by only looking at data from 2014-01-01 data = full_resampled['2014-01-01':] |
Normierung
Wir normieren die Daten in das Intervall [0,1], was hauptsächlich der leichteren statistischen Handhabe dient. Zudem ist der Google-Wert arbiträr, wir wollen ihm also nur relativ zu sich selbst Vertrauen schenken.
|
1 2 3 4 5 6 7 8 9 10 11 |
#Normalise the Data def normalize(df): result = df.copy(deep=False) for feature_name in df.columns: max_value = df[feature_name].max() min_value = df[feature_name].min() result[feature_name] = (df[feature_name] - min_value) / (max_value - min_value) return result data_normalized = normalize(data) |
|
1 2 3 |
#Plotting the full and normalized dataset plotData(data_normalized, secondaryData='Infra', leftLabel='Google News Trend (Norm)', rightLabel='Infratest Sonntagsfrage (Norm)') |
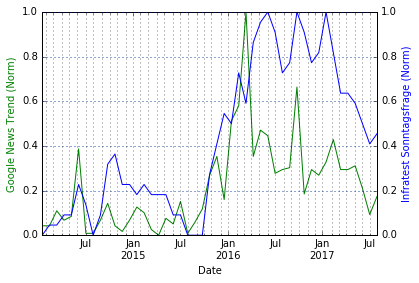
|
1 2 |
data_normalized.corr()['Infra']['Google'] |
|
1 2 |
0.68139695817025181 |
Normierte und abgeschnittene Daten
Die Korrelation der Daten ab 2014 ist mit 0.68 relativ stark (die Normierung hat hierauf keinen Einfluss).
Zeitverschiebung der Google-News
Wir werden nun die News-Trends schrittweise um je einen Tag verschieben und den Shift festhalten, der die größte Korrelation realisiert.
Hierfür gehen wir wie folgt vor:
- Abschneiden der Google- und Infratest-Daten vor 2014
- Verschieben des Google-Datensatzes um von -50 bis +50 Tagen und jeweils:
- Vereinigen des geshifteten Google-Datensatzes mit dem von Infratest
- Berechnen der Korrelation des vereinigten Satzes
- Speichern von Verschiebung gegen Korrelation
- Auslesen der Verschiebung mit maximaler Korrelation
- Normieren und Analysieren des Datensatzes mit maximaler Korrelation
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
shiftRange = range(-50,51) correlationDict = {} #Starting anew with the two datasets google = pd.read_csv('GoogleNews-DateTrend.csv', delimiter=";") infra = pd.read_csv('Infratest-DateValue.csv', delimiter=";") infra['Date'] = pd.to_datetime(infra['Date'], format="%d.%m.%y") google['Date'] = pd.to_datetime(google['Date']) infra.set_index(['Date'], inplace=True) google.set_index(['Date'], inplace=True) #Cutting of everything before 2014 infra = infra[:'2014-01-01'] google = google[:'2014-01-01'] #Looping over shiftRange, shifting google, combining datasets, computing correlation for shift in shiftRange: shiftedSet = google.copy(deep=False) shiftedSet.index = shiftedSet.index + pd.DateOffset(days=shift) combined = shiftedSet.join(infra, how='outer') combined_resampled = combined.resample('4W').mean() correlationDict[shift] = combined_resampled.corr()['Infra']['Google'] shiftOfHighestCorrelation = sorted(correlationDict, key=correlationDict.get, reverse=True)[0] highestCorrelation = correlationDict[shiftOfHighestCorrelation] |
|
1 2 |
print("Die größte Korrelation finden wir bei einer Verschiebung um %d Tage. Die Korrelation lautet dann %f." %(shiftOfHighestCorrelation, highestCorrelation)) |
|
1 2 |
Die größte Korrelation finden wir bei einer Verschiebung um 29 Tage. Die Korrelation lautet dann 0.768577. |
Vorläufiges Resultat
Wir finden die maximale Korrelation von 0.769 bei einer Verschiebung der Google-Daten um 29 Tage. Zur Veranschaulichung plotten wir diesen Datensatz nochmals.
|
1 2 3 4 5 6 7 |
shiftedGoogle = google.copy(deep=False) shiftedGoogle.index = shiftedGoogle.index + pd.DateOffset(days=shiftOfHighestCorrelation) combined = shiftedGoogle.join(infra, how='outer') combined_resampled = combined.resample('4W').mean() combined_resampled_normalized = normalize(combined_resampled) plotData(combined_resampled_normalized, secondaryData='Infra', leftLabel="Google News Trend, verschoben um %d Tage und normiert" %shiftOfHighestCorrelation, rightLabel='Infratest Sonntagsfrage, normiert') |
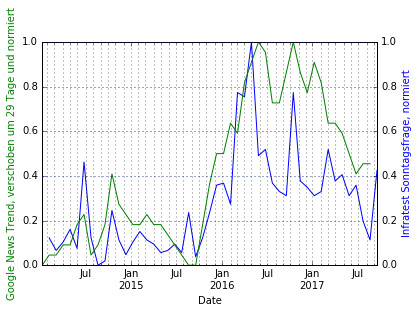
Achtung: Die Achsenbeschriftungen sind fälschlicherweise vertauscht!
Zusammenfassung
Die gewonnenen Daten weisen darauf hin, dass die Berichterstattung dem Umfrageverhalten um ca. 29 Tage vorauseilt. Naheliegend ist die Erklärung als Effekt der Aufmerksamkeitsökonomie: Spült die Presse (wohlgemerkt sind im Google News Trend nicht nur die großen Zeitungen enthalten, sondern auch Blogger, Twitter, Newsgroups, etc. Es handelt sich also nicht zwingend um eine Metrik der Präsenz in den Leitmedien, vielmehr enthält dieser Trend auch das „Rauschen“ in den Medien und sozialen Netzwerken) die AfD wieder in das öffentliche Bewusstsein, folgen die Wahlberechtigten mit einer Latenz von etwa einem Monat nach.
Natürlich sind die verwendeten Datensätze nicht besonders aussagekräftig und es liegen sicher multikausale Effekte vor. Jedoch erscheint eine so starke Korrelation (0.769) bei einer etwa einmonatigen Latenz mehr als zufällig.
Weitere Untersuchungen
Man sollte zunächst eine ähnliche Analyse für die anderen deutschen und auch europäischen Parteien durchführen. Eine Verbesserung der Daten wäre ebenfalls wünschenswert. Erklärungsmodelle sollten gefunden und verglichen werden. Ebenso ist eine detailliertere statistische Analyse der Daten notwendig.
Hallo Robin,
um zu testen, ob die Korrelation tatsächlich signifikant von 0 verschieden ist, kann man das Problem mal mit
zwei voneinander unabhängigen Zeitreihen simulieren. Ich kann kein Python, sondern nutze R [aber R-Code ist
eigentlich ganz gut lesbar]. Eine Korrelation von 0.77 oder mehr kommt bei zwei unabhängigen Zeitreihen mit Gauss-Rauschen in in mehr als 5% der Fälle vor. Dein Ergebnis ist somit nicht signifikant. Bei Fragen kannst du mir gerne eine E-Mail schreiben.
Viele Grüße, Daniel.
set.seed(123)
# ca. 3 Jahre monatliche Daten ergeben 36 Datenpunkte
calc_corr <- function(n = 36, trim = 0, sd = 1){
x <- rnorm(1); y <- rnorm(1);
for(i in 1:(n-1)){x <- c(x, x[i] + rnorm(1, sd = sd))}; rm(i)
for(i in 1:(n-1)){y <- c(y, y[i] + rnorm(1, sd = sd))}; rm(i)
if(trim == 0) return(cor(x,y))
opt <- sapply(0:trim, function(i) cor(x[1:(n-i)],y[(i+1):n]))
return(max(opt))
}
# Ohne Optimierung:
res = 0.77)) / 10000
# 0.0517 (p-Wert nicht signifikant, da > 0.05)
# Mit 2-Wochen-Optimierung:
res2 = 0.77)) / 10000
# 0.0633 (p-Wert nicht signifikant, da > 0.05)
Hi Daniel,
danke für deinen Kommentar!
Ja, völlig klar, mit den vorhandenen Daten kann ich nicht von Signifikanz sprechen. Signifikanz ist aber auch nur bedingt der relevante Blickwinkel. Die Korrelation ist hier ja insbesondere im Vergleich mit den anderen Parteien auffällig hoch und – das habe ich erwähnt – wächst mit der Zeitverschiebung der Trend-Daten.
Die Korrelationen, die du berechnest, sind ja auch immerhin unter 10%, damit liegen wir in meinem Fall natürlich unter der „wissenschaftlichen“ 5%-Signifikanz, aber selbst die wäre mir als Physiker mit meinen 6 Sigma immer noch viel zu „schlecht“.
Letztlich ist es denke ich klar, dass die Daten für keine belastbare Statistik herhalten. Der Trend ist aber doch deutlich und insbesondere im Vergleich mit den anderen Parteien (siehe meinen anderen Beitrag dazu) auffallend.